Hur detta skall se ut beror på var du återanvänder informationen. Det kan exempelvis se ut så här:
Ronny Gunnarsson. "Att välja statistisk metod" [på INFOVOICE.SE]. Tillgänglig på: https://infovoice.nu/att-valja-statistisk-metod/. Informationen hämtad July 29, 2025.
| Rekommenderad läsning före denna webbsida | Vad du får ut av att läsa denna webbsida |
|---|---|
| Denna webbsida berättar om olika statistiska metoder och när man kan använda dem. Att läsa denna sidan (några gånger) kommer att ge dig en förståelse av de val man måste göra och hur man väljer statistisk metod. Du kommer sannolikt kunna välja statistisk metod för ditt eget projekt när du studerat detta en stund. Glöm inte att först gå igenom lästipsen som ger dig en grund för att förstå denna sidan. |
Statistikens fågelperspektiv
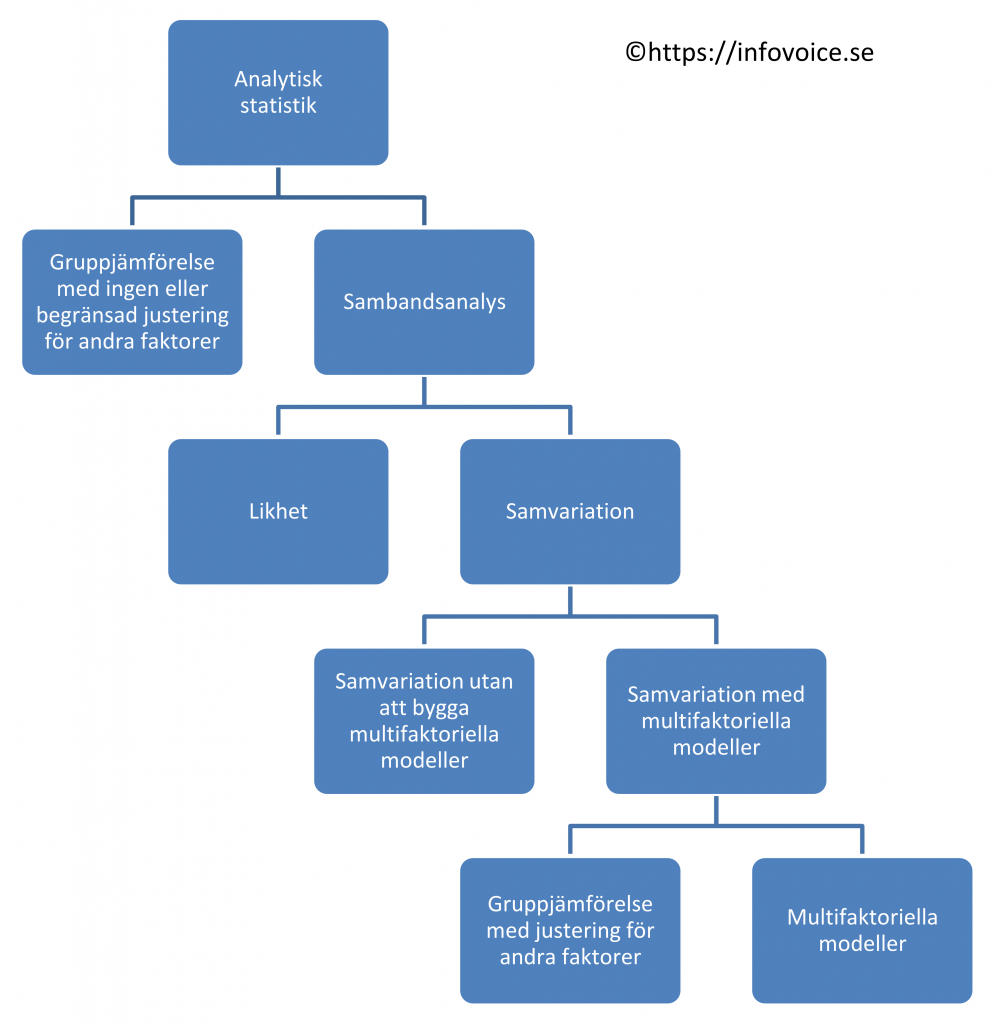
Statistik består av två huvuddelar; beskrivande statistik och analytisk statistik. Beskrivande statistik försöker beskriva observationerna, vanligen genom att ange ett centralmått och ett spridningsmått. Analytisk statistik försöker dra slutsatser från observationerna.
Denna webbsida handlar om val av statistisk metod för den analytiska statistiken. Figuren visar ett fågelperspektiv över analytisk statistik som har två huvudinriktningar:
- Gruppjämförelser (en grupp mot ett fixt värde, matchade eller omatchade grupper) med ingen eller begränsad justering för andra faktorer.
- Sambandsanalys. Den görs alltid i en enda grupp (även om det skenbart kan se ut som flera grupper).
Parametriska eller icke-parametriska metoder?
Statistiska metoder som används inom analytisk statistik kan delas upp i parametriska respektive icke-parametriska metoder. Så när du är klar med den beskrivande statistiken är det dags att bestämma om den analytiska statistiken skall använda parametriska eller icke-parametriska metoder (följ länken och läs mer om detta innan du läser vidare här).
Parametriska test kallas de test som har vissa lite hårdare krav framför allt på hur mätvärdena skall vara fördelade. Det första och viktigaste kravet är att variablerna skall mätas med intervallskala. Dessutom kräver de att variabeln skall vara normalfördelad. Dessutom krävs om man jämför två eller fler grupper att variansen (spridningen) i de olika grupperna är ungefär lika stor. Om din variabel mäts med intervallskalan bör du undersöka om dina mätvärden uppfyller villkoren för att få använda parametriska tester.
Grundregeln är att använda parametriska metoder om dina observationer uppfyller villkoren för detta. I annat fall använd icke-parametriska metoder. Parametriska metoder är lite känsligare och har större chans att hitta vad du letar efter. Det är vanligt att man i en och samma studie analyserar vissa variabler med parametriska metoder och andra variabler med icke-parametriska.
Gruppjämförelse eller samvariationsanalys?
Det kan bevisas att göra en enkel gruppjämförelse eller att utvärdera samma sak med “samvariation med multifaktoriella modeller” (vanligen med någon sorts regressionsanalys) ger samma resultat. Det är faktiskt så att de flesta gruppjämförelser är egentligen bara ett specialfall av samvariation med multifaktoriella modeller. Spelar det då någon roll om jag använder statistiska metoder för gruppjämförelse eller samvariation med multifaktoriella modeller? Ja det gör det!
Det är ganska vanligt att det finns störande faktorer som påverkar resultatet vid en gruppjämförelse. Exempel på sådana störande faktorer kan vara kön, ålder, att vara rökare, att ha sockersjuka, etc. Om du använder gruppjämförelse vill du antagligen göra sub-analys av olika undergrupper för att se hur de påverkar resultatet. Detta medför några allvarliga problem:
- Du måste antagligen göra flera separata gruppjämförelser som då leder till flera p-värden (ett för varje gång du gör en gruppjämförelse). Låt oss som exempel anta att du har tre variabler där du kan utvärdera skillnad mellan grupperna. Låt oss anta att dessa utfallsvariabler är minskning i dödlighet, minskning i andelen patienter som får hjärtinfarkt och slutligen minskning i kolesterolnivå i blodet. Detta medför då tre olika p-värden (om vi använder p-värden för att visa på skillnad mellan grupperna) när vi analyserar skillnad mellan våra två grupper, ett p-värde för varje utfallsvariabel. Om vi dessutom vill göra analys av undergrupper för kön, ålder (över eller under 65 år), om patienten har sockersjuka och om de är rökare behöver vi räkna fram 3*2*2*2*2=48 p-värden.
Att räkna fram många p-värden kräver justering av signifikansnivån på grund av multipel testning. Med många undergrupper blir det snabbt så att justeringen av signifikansnivån blir så stor att det blir mycket svårt, kanske omöjligt, att påvisa en skillnad mellan grupperna. - När du delar upp i undergrupper blir antalet tillgängliga observationer i varje undergrupp mycket mindre och det ökar risken för att dina statistiska analyser har för litet antal observationer för att uppnå en rimlig statistisk styrka.
Alternativet till att göra gruppjämförelser är att använda samvariation med multifaktoriella modeller. Du kan då ta med alla relevanta variabler i en enda statistisk körning som omfattar samtliga observationer. Du gör då en separat analys för var och en av utfallsvariablerna (utfallsvariablerna kallas i den beräkningen beroende variabel). Alla andra variabler såsom kön, ålder, sockersjuka och rökning samt grupptillhörighet tas med som oberoende variabler. I ovanstående exempel innebär det framräknande av 3*(1+1+1+1+1)=15 mått (såsom p-värden eller odds ratio, etc) på vad som betyder något i gruppjämförelsen. Storleken på justeringen av signifikansnivån som du måste göra för att producera 15 mått (exempelvis p-värden) är mycket mindre jämfört med om du räknar fram 48 mått.
Slutsatsen är att använd enkel gruppjämförelse med ingen justering för andra faktorer om du inte har något behov av att justera för andra faktorer. Detta inträffar bara i väl genomförda randomiserade kontrollerade studier. I alla andra situationer (och även ibland när du har gjort en randomiserad kontrollerad studie) så är det mycket bättre att göra gruppjämförelse genom att analysera samvariation med multifaktoriella modeller. detta är speciellt viktigt när man jämför grupper genom historiskt insamlade data, så kallade retrospektiva studier (exempelvis journalgranskningar som görs i efterhand) där störande faktorer alltid finns.
Viktiga aspekter att beakta i olika situationer
Randomiserade kontrollerade studier (RCT)
Huvudsyftet med randomisering till olika grupper är att minska risken för systematiska felkällor. Huvudsyftet med randomisering är inte att skapa grupper som är lika, även om randomisering oftast har den önskade bieffekten. Det är viktigt att förstå att en skillnad mellan grupper kan uppstå även om individerna fördelas slumpmässigt (randomiseras) till de olika grupperna. Om en skillnad mellan grupperna uppstår kan man överväga att justera för detta genom att göra gruppjämförelsen med samvariation med multifaktoriella modeller. Om du använder samvariation med multifaktoriella modeller låter du grupptillhörighet vara en av de oberoende variablerna medan de variabler där grupperna skiljer sig åt i baseline (första mätningen) också tas med som oberoende variabler.
Dikotoma tester för screening eller diagnostik
Normalt behövs en “Gold standard” (=referensmetod) för att utvärdera ett nytt test med sensitivitet, specificitet, likelihood ratio eller prediktiva värden. Gold standard är en accepterad referensmetod som förhoppningsvis också ger ett bra mått på det sanna värdet som skall mätas.
Det är vanligt att det test vi vill utvärdera mäter något som inte nödvändigtvis innebär att individen är sjuk. Exempelvis kan man bära bakterier men en sjukdom kan bero på något annat, exempelvis ett virus. Vi måste alltså förstå att i vissa fall är det en skillnad mellan att påvisa en bakterie och att försöka bevisa att personen är sjuk av just den bakterien. Titta gärna på denna presentation som försöker exemplifiera detta:
Att klicka på bilden nedan tar dig till YouTube där videon spelas upp. Observera att Youtube’s hemsida kommer att lagra “kakor (cookies)” på din dator. Du kan läsa mer om detta på vår sida om GDPR och “kakor (cookies)”.

För varje test som skall utvärderas bör man diskutera vad är det egentligen som gold standard påvisar, är det närvaro av en markör eller närvaro av en sjukdom.
Antag att vi vill jämföra ett nytt väldigt bra test med en etablerad referensmetod (som vi utnämner till gold standard). Om det nya testet är bättre än vårt referenstest kommer det nya testet att felaktigt verka som dåligt. Skälet är att varje gång det nya testet och referensmetoden inte stämmer överens klassas det som ett fel hos det nya testet fast det i verkligheten kanske är tvärtom. Kom alltså ihåg att alltid ifrågasätta om referensmetoden verkligen är lika bra eller bättre än det test man vill utvärdera.
Sensitivitet och specificitet talar om hälsotillståndet hos det test du vill utvärdera, något som är mycket intressant för de som utvecklar och tillverkar tester. Prediktiva värden informerar om hälsotillståndet hos patienten och det är mycket mer intressant för sjukvårdspersonal.
Fall-kontroll eller kohortstudier
Detta görs ibland som eftergranskning av patientjournaler och man vill veta om ett sätt att handlägga patienter är bättre eller sämre än ett annat sätt. Låt oss diskutera ett exempel: Vid operation av njursten används antingen öppen kirurgi, titthålskirurgi eller stötvågsbehandling (det finns fler metoder men för diskussionens skull håller vi oss till dessa tre). Någon har fått i uppgift att titta på hur det har gått för patienter som opererades på det ena eller andra sättet . Detta är inte en randomiserad kontrollerad studie och detta är huvudproblemet. Konsekvensen i detta exempel är att vi jämför tre grupper av patienter som inte är jämförbara. Skillnader i resultat kan mycket väl bero på skillnader mellan grupperna istället för skillnader i effekten av de olika behandlingarna.
Eftergranskning av journaler eller databaser som innehåller information om patienter används ibland i syftet att jämföra olika behandlingar. Det är viktigt och komma ihåg att det då nästan alltid finns störande faktorer som man bör ta hänsyn till genom att göra gruppjämförelser med samvariation med multifaktoriella modeller. En specialvariant av sistnämnda är “propensity score matching“.
Samvariation med multifaktoriella modeller
Det är vanligt att man vill förutsäga risken för att något skall hända. Det kan exempelvis handla om förändrad livskvalitet, att en sjukdom skall uppstå eller bli försämrad eller om död. Du gör då en körning av en statistisk metod för varje utfallsvariabel du har (kallas ofta beroende variabel). Du undersöker då hur ett antal oberoende variabler korrelerar till din utfallsvariabel. Om din utfallsvariabel är dikotom (typ 0/1, eller sjuk / frisk) vill du antagligen använda logistisk regression. Om din utfallsvariabel är tid till något (exempelvis försämring/förbättring eller död) vill du antagligen använda Cox regression.
Att använda samvariation med multifaktoriella modeller är ett bra alternativ till att göra fall-kontroll studier. Grupptillhörighet blir då en av flera oberoende variabler. Tolkningen av samband blir att det finns en “samvariation” snarare än orsak-verkan. Sistnämnda kräver ofta randomiserade kontrollerade studier för att fastställas.
Specifika råd för att välja statistisk metod
Samvariation
Samvariation analyseras nästan alltid med någon form av regressionsanalys. I regressionsanalyser talar man om beroende och oberoende variabler. Man letar efter hur stor del av variationen i den beroende variabeln som förklaras av variationer i de oberoende variablerna. I de flesta regressionsanalyser har man en enda beroende variabel som undersöks tillsammans med en eller flera oberoende variabler. Det är vanligt att man undersöker vad som samvarierar med flera beroende variabler men då undersöker man nästan alltid en beroende variabel i taget.
Det finns väldigt komplicerade statistiska analyser som samtidigt utvärderar vad som samvarierar med flera beroende variabler. Man kan också analysera vad som samvarierar med en virtuell beroende variabel (en tänkt beroende variabel som man tror finns men som inte direkt går att mäta).
Samvariation med en beroende variabel
Samvariation utan att bygga multifaktoriella modeller
Här handlar det om att se hur två variabler (en beroende och en oberoende) samvarierar. När det bara är två variabler brukar man sällan tala om vilken som är beroende respektive oberoende variabel. Så fort det är mer än två variabler inblandade blir det multifaktoriella modeller.
Klicka för att rulla ner och se vilka statistiska test som är lämpliga| Mätskala | Lämpliga statistiska test | Kommentar |
|---|---|---|
| Nominalskala - Båda variablerna kan bara anta två värden vardera (dikotom variabel). Detta är icke-parametriska tester. | Odds ratio (OR) | Vanligt |
| Logistisk regression | Bara ett annat sätt att räkna fram odds ratios. Ger samma svar som ovan. | |
| Relativ risk (RR) | Vanligt | |
| Phi coefficient | ||
| Craemer's Phi coefficient = Craemer's V coefficient | ||
| Yule coefficient of association = Yule's Q | ||
| Nominalskala - Minst en av variablerna kan anta >2 värden vardera. Detta är icke-parametriska tester. | Craemer's Phi coefficient = Craemer's V coefficient | |
| Ordinalskala - Båda mäts med ordinalskalan (har ordning men inte lika stora skalsteg). Detta är icke-parametriska tester. | Spearmann’s rangkorrelation | Mycket vanligt test |
| Gamma coefficient = Gamma statistic = Goodman and Kruskal's gamma | ||
| Kendall’s coefficient of concordance = Kendall’s tau | ||
| Somer’s D | ||
| Intervall- eller kvotskala - Båda mäts med Intervall- eller kvotskala (har ordning och lika stora skalsteg) men åtminstone en av dem är snedfördelad. Detta är icke-parametriska tester. | Spearmann’s rangkorrelation | Mycket vanligt test |
| Intervall- eller kvotskala - Båda mäts med Intervall- eller kvotskala (har ordning och lika stora skalsteg) och båda är normalfördelad. Detta är parametriska tester. | Pearson’s korrelation | Mycket vanligt test |
| En av variablerna mäts enligt nominalskalan och är dikotom. Den andra mäts enligt ordinalskalan eller enligt intervall/kvotskalan men är då snedfördelad. Detta är icke parametriska tester. | Logistisk regression | Mycket vanligt test |
| En av variablerna mäts enligt nominalskalan och är dikotom. Den andra mäts enligt intervall/kvotskalan och är normalfördelad. Detta är parametriska tester. | Eta-squared | (Detta är sambandsanalysens motsvarighet till gruppjämförelsens one-way ANOVA) |
Samvariation med multifaktoriella modeller
Här har vi mer än två variabler. Man utnämner då alltid en av dem till beroende variabel och de övriga kallas då oberoende variabler.
Klicka för att rulla ner och se vilka statistiska test som är lämpliga| Mätskala för den beroende variabeln | Lämpliga statistiska test | Kommentar |
|---|---|---|
| Nominalskala med två alternativ (dikotom variabel) | Omatchad logistisk regression = Unconditional binary logistic regression | Vanligt test |
| Propensity score matching | Används mestadels när man vill göra gruppjämförelse mellan grupper fast det finns mängder av konfunderande variabler man behöver ta hänsyn till. | |
| Mantel-Haenszels stratifierade analys | Endast om alla oberoende variabler är dikotoma. Logistisk regression är ett bättre alternativ. | |
| Nominalskala med >2 alternativ | Multinominal logistic regression =multiclass logistic regression | |
| Propensity score matching | Med hjälp av olika knep kan man få propensity score matching att fungera med >2 grupper i den beroende variablen. | |
| Ordinalskala (har ordning men inte lika stora skalsteg) | Ordered logistic regression = Ordinal regression | |
| Omatchad logistisk regression = Unconditional binary logistic regression | Som alternativ kan man introducera en cut-off och istället använda vanlig logistisk regression. | |
| Intervall- eller kvotskala | Linjär regression = Linear regression | Detta kallas även "kovariansanalys" = "analysis of covariance (ANCOVA)" om minst en av de oberoende variablerna är dikotom. |
| Propensity score matching | ||
| Omatchad logistisk regression = Unconditional binary logistic regression | Som alternativ kan man introducera en cut-off och istället använda vanlig logistisk regression. | |
| Tid till en händelse (detta är ett specialfall av intervall- eller kvotskala) | Cox proportional hazards regression |
Samvariation med flera beroende variabler
Detta är avancerad statistik. Exempel är faktoranalys eller multivariat probit analys.
Samvariation med virtuell beroende variabel
Detta är avancerad statistik. Exempel är faktoranalys
Gruppjämförelser (ej justering för andra faktorer)
Något mätvärde jämförs mellan grupperna. Detta mätvärde har olika namn såsom: resultatvariabel, utfallsvariabel, utfallsmått eller beroende variabel. Grupptillhörighet och andra variabler man ibland vill justera för kallas oberoende variabler.
- Fastställ hur många variabler (faktorer) används för att indela deltagarna/observationerna i grupper:
-Noll-faktor design: Inga variabler används för gruppindelning. En enda grupp jämförs då med ett fastställt målvärde. Alternativt görs en före-efter-jämförelse i en enda grupp.
-En-faktor design: Här används en variabel (faktor) för att indela observationer/deltagare i grupper. Oftast indelas observationerna/deltagarna i två grupper (men det kan vara fler). Detta är den vanligaste gruppjämförelsen.
-Två-faktor design: Om två faktorer (exempelvis olika behandlingar som en faktor och olika timing/initierande av behandling som en annan faktor) används för att indela observationer/deltagare i grupper. Om varje faktor som indelar observationerna/deltagarna i grupper hade två alternativ vardera skulle vi få en två-faktor design med fyra grupper. Det skulle fortfarande vara en två-faktor design om varje faktor som kopplas till gruppindelning hade tre alternativ vardera men då skulle vi få en två-faktor design med nio grupper.
-N-factor design: Det finns studier där man har fler än två faktorer som styr gruppindelning. Dessa studier är komplicerade och därför mycket ovanliga. - Om du har åtminstone två grupper (åtminstone en en-faktor design) så klarlägg om grupperna är matchade eller omatchade.
- Klarlägg vilka mätskalor som är lämplig för dina variabler. Detta påverkar valet av statistisk metod.
- Om intervall- eller kvotskalan används för en del variabler är dessa observationer normalfördelade? Om svaret är ja kan du använda parametriska statistiska metoder, annars får du välja icke-parametriska metoder..
- Om nominalskalan används för resultatvariabeln har resultatvariabeln bara två alternativ (dikotom variabel) eller finns fler alternativ?
Gruppjämförelse – Nollfaktordesign (Zero factor design)
Klicka för att rulla ner och se vilka statistiska test som är lämpliga| Mätskala för den beroende variabeln | Lämpliga statistiska test | Kommentar |
|---|---|---|
| Nominalskala med två alternativ (dikotom variabel). Detta är icke-parametriska test. | Chi-square | Kräver minst 5 observationer i varje cell. |
| Z-test | ||
| Nominalskala med >2 alternativ. Detta är icke-parametriska test. | Chi-square | Kräver minst 5 observationer i varje cell. |
| Ordinalskala (har ordning men inte lika stora skalsteg). Detta är icke-parametriska test. | Teckenrangtest = Wilcoxon one sample signed rank sum test | |
| Intervall- eller kvotskala som inte uppfyller villkoren för parametriska statistiska test (oftast snedfördelning av observationerna). Detta är icke-parametriska test.. | Teckenrangtest = Wilcoxon one sample signed rank sum test | |
| Z-test | ||
| Intervall- eller kvotskala som uppfyller villkoren för parametriska statistiska test (oftast normalfördelning av observationerna) | Student's t-test - one sample t-est | |
| (Z-test) | T-test ovan är känsligare. | |
| Tid till en händelse (detta är ett specialfall av intervall- eller kvotskala) | One-Sample Log rank Test | |
| Kaplan-Meyer curves | Detta är en teknik för att i en figur presentera vad som händer över tid i en eller flera grupper. Det är inget statistiskt test och levererar inget p-värde. |
Gruppjämförelser – Enfaktordesign
Gruppjämförelse – Enfaktordesign 2 omatchade grupper
Klicka för att rulla ner och se vilka statistiska test som är lämpliga| Mätskala för den beroende variabeln | Lämpliga statistiska test | Kommentar |
|---|---|---|
| Nominalskala med två alternativ (dikotom variabel) | Chi-square | Kräver minst 5 observationer i varje cell. Om du har färre gör på Fisher's exakta test istället. |
| Fisher's exact test | Har i princip inga krav på minsta antal. ger liknande (men mer exakt) svar som chi-två. | |
| Nominalskala med >2 alternativ | Chi-square | Kräver minst 5 observationer i varje cell. |
| Ordinalskala (har ordning men inte lika stora skalsteg) | Mann-Whitney's test = Wilcoxon two unpaired test = Rank sum test | Mycket vanligt test |
| Fisher's permutation test | ||
| Cochran–Mantel–Haenszel (CMH) test | ||
| Kruskal-Wallis test | Kan jämföra >2 grupper. Vid bara 2 grupper får man samma resultat som Mann-Whitney's test. Detta är den icke parametriska motsvarigheten till one way ANOVA. | |
| Intervall- eller kvotskala som inte uppfyller villkoren för parametriska statistiska test (oftast snedfördelning av observationerna) | Mann-Whitney's test = Wilcoxon two unpaired test = Rank sum test | Mycket vanligt test |
| Fisher's permutation test | ||
| Cochran–Mantel–Haenszel (CMH) test | ||
| Z-test | ||
| Kruskal-Wallis test | Kan jämföra >2 grupper. Vid bara 2 grupper får man samma resultat som Mann-Whitney's test. Detta är den icke parametriska motsvarigheten till one way ANOVA. | |
| Intervall- eller kvotskala som uppfyller villkoren för parametriska statistiska test (oftast normalfördelning av observationerna) | Student's t-test - two sample unpaired test | Mycket vanligt test. Klarar bara två omatchade grupper. Se nedan om du har >2 grupper. |
| One way analysis of variance | One way ANOVA används om det är fler än två omatchade grupper i ett enfaktorförsök. Om det bara är två omatchade grupper får man samma resultat med "Student's t-test - two sample unpaired test". | |
| Cohen's d | ||
| Z-test | ||
| Tid till en händelse (detta är ett specialfall av intervall- eller kvotskala) | Log rank test = Mantel–Cox test = time-stratified Cochran–Mantel–Haenszel test | Log rank test används om man har två omatchade grupper och inget behov av att justera för andra störande faktorer. |
| Kaplan-Meyer curves | Detta är en teknik för att i en figur presentera skillnader i tid till händelse mellan grupper. Det är inget statistiskt test och levererar inget p-värde. | |
| Cox proportional hazards regression | Cox proportional hazards regression används om man vill jämföra omatchade grupper och dessutom justera för störande faktorer. |
Gruppjämförelse – Enfaktordesign 2 matchade grupper
Klicka för att rulla ner och se vilka statistiska test som är lämpliga| Mätskala för den beroende variabeln | Lämpliga statistiska test | Kommentar |
|---|---|---|
| Nominalskala med två alternativ (dikotom variabel) | Teckentest (=Signs test) | |
| McNemars test | Teckentest fungerar också och är lite bättre. | |
| Stuart-Maxwells test | Stuart-Maxwells test kan även användas om du har >2 matchade grupper. | |
| Nominalskala med >2 alternativ | --- | Denna situation uppstår sällan. Skulle det inträffa bör skalan göras om till dikotom skala eller ordinalskala. |
| Ordinalskala (har ordning men inte lika stora skalsteg) | Teckentest (=Signs test) | |
| Fisher´s parade permutationstest | ||
| Intervall- eller kvotskala som inte uppfyller villkoren för parametriska statistiska test (oftast snedfördelning av observationerna) | Teckentest (=Signs test) | |
| Z-test | ||
| Fisher´s parade permutationstest | ||
| Intervall- eller kvotskala som uppfyller villkoren för parametriska statistiska test (oftast normalfördelning av observationerna) | Student's t-test - one sample unpaired test = Student's t-test paired t-test | Mycket vanligt test. Klarar bara två matchade grupper. |
| (Z-test) | ||
| Tid till en händelse (detta är ett specialfall av intervall- eller kvotskala) | (?) |
Gruppjämförelse – Enfaktordesign >2 omatchade grupper
Klicka för att rulla ner och se vilka statistiska test som är lämpliga| Mätskala för den beroende variabeln | Lämpliga statistiska test | Kommentar |
|---|---|---|
| Nominalskala med två alternativ (dikotom variabel) | Chi-square | Kräver minst 5 observationer i varje cell. |
| Nominalskala med >2 alternativ | Chi-square | Kräver minst 5 observationer i varje cell. |
| Ordinalskala (har ordning men inte lika stora skalsteg) | Kruskal-Wallis test one way analysis of variance | Detta är den icke parametriska motsvarigheten till one way ANOVA. (Kan jämföra >2 grupper. Vid bara 2 grupper får man samma resultat som Mann-Whitney's test.) |
| Intervall- eller kvotskala som inte uppfyller villkoren för parametriska statistiska test (oftast snedfördelning av observationerna) | Kruskal-Wallis test one way analysis of variance | Detta är den icke parametriska motsvarigheten till one way ANOVA. (Kan jämföra >2 grupper. Vid bara 2 grupper får man samma resultat som Mann-Whitney's test.) |
| Intervall- eller kvotskala som uppfyller villkoren för parametriska statistiska test (oftast normalfördelning av observationerna) | One way analysis of variance = one way ANOVA | One way ANOVA används om det är fler än två omatchade grupper i ett enfaktorförsök. (Om det bara är två omatchade grupper får man samma resultat med "Student's t-test - two sample unpaired test".) |
| Tid till en händelse (detta är ett specialfall av intervall- eller kvotskala) | Log rank test = Mantel–Cox test = time-stratified Cochran–Mantel–Haenszel test | Log rank test används om man har omatchade grupper (i ett enfaktorförsök) och inget behov av att justera för andra störande faktorer. |
| Kaplan-Meyer curves | Detta är en teknik för att i en figur presentera skillnader i tid till händelse mellan grupper. Det är inget statistiskt test och levererar inget p-värde. | |
| Cox proportional hazards regression | Cox proportional hazards regression används om man vill jämföra omatchade grupper och dessutom justera för störande faktorer. |
Gruppjämförelse – Enfaktordesign >2 matchade grupper
Klicka för att rulla ner och se vilka statistiska test som är lämpliga| Mätskala för den beroende variabeln | Lämpliga statistiska test | Kommentar |
|---|---|---|
| Nominalskala med två alternativ (dikotom variabel) | Stuart-Maxwells test | Motsvarar McNemars test men klarar >2 matchade grupper |
| Nominalskala med >2 alternativ | (Denna situation uppstår förmodligen aldrig. Skulle det inträffa bör skalan göras om till dikotom skala eller ordinalskala) | |
| Ordinalskala (har ordning men inte lika stora skalsteg) | Friedman´s test | Enfaktorförsöket omvandlas till ett tvåfaktorförsök genom att grupperna betraktas som en variabel och individerna som en annan. Analysera sedan med Friedmann's test som om det vore ett tvåfaktorförsök. |
| Intervall- eller kvotskala som inte uppfyller villkoren för parametriska statistiska test (oftast snedfördelning av observationerna) | Friedman´s test | Enfaktorförsöket omvandlas till ett tvåfaktorförsök genom att grupperna betraktas som en variabel och individerna som en annan. Analysera sedan med Friedmann's test som om det vore ett tvåfaktorförsök. |
| Intervall- eller kvotskala som uppfyller villkoren för parametriska statistiska test (oftast normalfördelning av observationerna) | Två-vägs-ANOVA | Enfaktorförsöket omvandlas till ett tvåfaktorförsök genom att grupperna betraktas som en variabel och individerna som en annan. Analysera sedan med två-vägs ANOVA som om det vore ett tvåfaktorförsök. |
| Tid till en händelse (detta är ett specialfall av intervall- eller kvotskala) | (?) |
Gruppjämförelse – Tvåfaktordesign
Gruppjämförelse – tvåfaktordesign omatchade grupper
Klicka för att rulla ner och se vilka statistiska test som är lämpliga| Mätskala för den beroende variabeln | Lämpliga statistiska test | Kommentar |
|---|---|---|
| Nominalskala med två alternativ (dikotom variabel). Detta är icke-parametriska test. | Omatchad logistisk regression = Unconditional binary logistic regression | Inkludera variablerna som styr gruppindelning och låt dem vara med som oberoende variabler (det blir minst 2 variabler för detta). Du kan sedan lägga till fler oberoende variabler som du vill justera för, ex vis kön, ålder, etc. |
| Nominalskala med >2 alternativ. Detta är icke-parametriska test. | Multinominal logistic regression =multiclass logistic regression | Inkludera variablerna som styr gruppindelning och låt dem vara med som oberoende variabler (det blir minst 2 variabler för detta). Du kan sedan lägga till fler oberoende variabler som du vill justera för, ex vis kön, ålder, etc. |
| Ordinalskala (har ordning men inte lika stora skalsteg). Detta är icke-parametriska test. | Friedman's test | |
| Ordered logistic regression = Ordinal regression | Inkludera variablerna som styr gruppindelning och låt dem vara med som oberoende variabler (det blir minst 2 variabler för detta). Du kan sedan lägga till fler oberoende variabler som du vill justera för, ex vis kön, ålder, etc. | |
| Intervall- eller kvotskala som inte uppfyller villkoren för parametriska statistiska test (oftast snedfördelning av observationerna). Detta är icke-parametriska test.. | Friedman's test | |
| Ordered logistic regression = Ordinal regression | Inkludera variablerna som styr gruppindelning och låt dem vara med som oberoende variabler (det blir minst 2 variabler för detta). Du kan sedan lägga till fler oberoende variabler som du vill justera för, ex vis kön, ålder, etc. | |
| Intervall- eller kvotskala som uppfyller villkoren för parametriska statistiska test (oftast normalfördelning av observationerna) | Tvåvägs variansanalys = Two-way analysis of variance (2-way ANOVA) | |
| Linjär regression = Linear regression | Inkludera variablerna som styr gruppindelning och låt dem vara med som oberoende variabler (det blir minst 2 variabler för detta). Du kan sedan lägga till fler oberoende variabler som du vill justera för, ex vis kön, ålder, etc. | |
| Tid till en händelse (detta är ett specialfall av intervall- eller kvotskala) | Cox proportional hazards regression | Inkludera variablerna som styr gruppindelning och låt dem vara med som oberoende variabler (det blir minst 2 variabler för detta). Du kan sedan lägga till fler oberoende variabler som du vill justera för, ex vis kön, ålder, etc. |
Gruppjämförelse – tvåfaktordesign matchade grupper
(Du hamnar sannolikt aldrig i denna situationen. Om du gör det konsultera statistiker.)
Utvärdera likhet
Typexemplet är att man vill utvärdera tester som används för screening eller diagnostik.
Klicka för att rulla ner och se vilka statistiska test som är lämpliga| Mätskala för den beroende variabeln | Lämpliga statistiska test | Kommentar |
|---|---|---|
| Nominalskala med två alternativ (dikotom variabel) | Kappakoefficient = Cohen's kappa coefficient | |
| Sensitivitet och Specificitet = Sensitivity and Specificity | Talar om hur det testet mår. Bra för tillverkare av tester. | |
| Likelihood ratio | Informerar om testet tillför något nytt. Bra för de som skapar riktlinjer. Detta är en specialvariant av odds ratio. | |
| Prediktivt värde av ett test = Predictive value of test | Talar om hälsotillståndet hos patienten (om det nu är patienter testet skall tillämpas på). Bra för de som handlägger patienter. | |
| Etiologiskt prediktivt värde (EPV) = Etiologic predictive value (EPV) | Prediktivt värde av ett test om man justerar för att personer kan vara falskt test-positiva bärare men sjuka av något annat. En gold standard (referensmetod) behövs inte. | |
| Nominalskala med >2 alternativ | Kappakoefficient = Cohen's kappa coefficient | |
| Ordinalskala (har ordning men inte lika stora skalsteg) | Kappakoefficient = Cohen's kappa coefficient | |
| Viktad kappakoefficient = Weighted kappa coefficient | ||
| Intervall- eller kvotskala | Limits of agreement | Kombineras ofta med att göra Bland-Altman plot |
| Bland-Altman plot = Difference plot = Tukey mean-difference plot | Detta är en grafisk presentation av hur två tester stämmer överens. | |
| Lin's Concordance correlation coefficient | ||
| Intra class correlation (=ICC) | (Det är oftast bättre att använda någon av ovanstående metoder) |
Referenser
Hur detta skall se ut beror på var du återanvänder informationen. Det kan exempelvis se ut så här:
Ronny Gunnarsson. "Att välja statistisk metod" [på INFOVOICE.SE]. Tillgänglig på: https://infovoice.nu/att-valja-statistisk-metod/. Informationen hämtad July 29, 2025.

